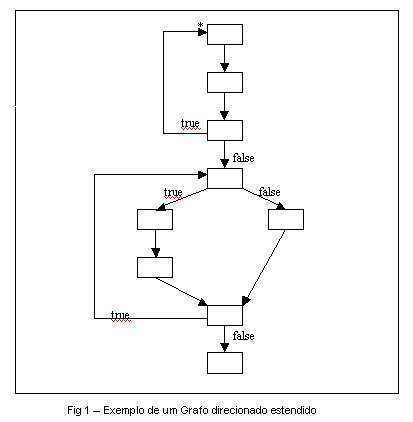
Def 2.1.1 : Um H-grafo H sobre N, A, e L é um par H= (M, V) , onde:

·        M é um subconjunto de N, não vazio e finito;

·        V é uma função de valor e conteúdo que mapeia M para A È {G' | G' é um grafo direcionado estendido sobre M e L}.

·        Assim, se 'n' é um nó de M, então V(n) é designado valor ou conteúdo de 'n'.

H-grafos são estruturas formais usadas para modelar programas e estruturas de dados.  A figura 1 mostra um exemplo de um grafo direcionado estendido. Na definição de LP a saída do tradutor (que também é o estado inicial do autômato) é um H-grafo, assim como são cada um dos demais estados através dos quais o autômato passa durante a execução do programa.

Os H-grafos representam melhor uma nova ordem da hierarquia dos grafos. Começando de qualquer nó de um H-grafo, podemos descer um nível, aplicando a função de valor V.  Após a aplicação de V, encontraremos um nó, que pode vir a ser um valor atômico em A ou um grafo.  Desta forma um H-grafo é organizado hierarquicamente por níveis.  Descendo um nível do grafo, nós podemos encontrar nós que já apareceram anteriormente em níveis mais altos do grafo.  De fato esta hierarquia pode ser recursiva, ou seja, um nó recém alcançado no grafo pode ser um nó pelo qual nós descendemos de um nível mais alto.

Este aspecto da definição do H-grafo permite uma modelagem natural de muitos construtores de linguagens de programação.

2.2  GramÁticas Pares

Uma gramática par é composta de um par de gramáticas formais cujas produções e símbolos não terminais estão relacionados um a um.  As duas gramáticas são chamadas de gramática à esquerda e gramática à direita, respectivamente.  Uma gramática par ou é uma gramática de string livre de contexto ou é uma gramática de grafo livre de contexto.

Uma gramática par G é uma quádrupla G= ( K, T, S, P ), onde:

· K é um conjunto finito de símbolos não terminais

· T é conjunto finito de símbolos terminais

· S Î K e é o símbolo inicial

· P é um conjunto de produções

Cada produção de P é composta de um par de produções de gramáticas livre de contexto de grafo ou string.  As produções são respectivamente uma à esquerda outra à direita.  O conjunto de todas as produções à esquerda de G define uma gramática livre de contexto, denominada gramática à esquerda de G.  Logo, esta gramática à esquerda de G define uma linguagem à esquerda de G.  A gramática à direita e a linguagem à direita de G são definidas com um raciocínio similar.

A linguagem L( G ) definida por uma gramática G consiste de um conjunto de pares ordenados de elementos das linguagens à direita e à esquerda, respectivamente de G.  Para gerar um par em L ( G ), começamos com o par ( S, S ), que consiste do símbolo inicial de G nas posições à esquerda e à direita.  Um produção ( S®a, S®a’) de G é escolhida.  A aplicação desta produção para o par ( S,S ), produz um novo par (a, a’) onde a e a’ contém os mesmos símbolos não terminais em correspondência 1-1.  Derivando desta maneira nós chegaremos a um par terminal ( w, w’) contendo símbolos não terminais, ( w, w’) é então um elemento de L ( G ), com w na linguagem à esquerda e w’ na linguagem à direita de G.

Para a definição de uma linguagem de programação o par ( w, w’) na linguagem definida por uma gramática par, w deve ser considerado como um programa de entrada e w’ a sua representação gráfica.  Logo, a gramática par G define a translação entre programas e sua representação gráfica correspondente.

2.2.1  GramÁticas de Grafos

Para a definição de linguagem de programação usando H-grafos  nós desejamos que uma gramática à direita de um par defina uma linguagem composta de H-grafos , enquanto que para a gramática à esquerda, a linguagem definida deve ser um conjunto de strings de caracteres representando programas sintaticamente corretos na linguagem.  Uma gramática livre de contexto normal é suficiente para a gramática à esquerda.  Porém a gramática à direita requer uma extensão do conceito de uma gramática livre de contexto normal para o de uma gramática livre de contexto de grafos, que é uma gramática livre de contexto que define uma linguagem composta de um conjunto de H-grafos

Uma gramática livre de contexto F é uma quádrupla F = ( K, A, S, R ) onde:

· K é um conjunto finito de não terminais

· A é um conjunto de terminais

· S Î K é o símbolo inicial

· R é um conjunto finito de produções

Cada produção em R é uma quíntupla ( C, H, G, I, O ) onde C Î K ( o não terminal à esquerda ) e H, G, I e O formam o lado direito da produção.  H = ( M, V ) é um H-grafo com átomos escolhidos de um conjunto K È A, G é um grafo direcionado estendido sobre M e A, com nó inicial I.  O, o nó final, é também um nó em G.

Uma gramática livre de contexto de grafos funciona praticamente da mesma maneira que uma gramática livre de contexto normal para gerar um grafo em sua linguagem.  Você começa com um nó que contém como seu valor o símbolo de início da gramática.  Cada regra da gramática de grafos especifica um símbolo não terminal à esquerda e um H-grafo à direita.  Estes grafos à direita podem conter outros nós com valores não terminais.  Quando todos estes nós forem substituídos por nós terminais, o grafo resultante é uma “linguagem de grafo” definida pela gramática.  A única dificuldade a mais no processo de geração vem da necessidade de especificar como “ligar” o grafo a ser substituído por um grafo já existente quando um nó não terminal é substituído por um grafo de com uma regra da gramática.  Em gramáticas de grafos simples, isto é feito simplesmente especificando um nó inicial e um nó final no grafo à direita de cada regra da gramática.  Quando um nó não terminal é substituído por um grafo, cada arco chegando neste nó não terminal é conectado ao nó inicial de um novo grafo, e cada arco saindo de um nó não terminal é conectado ao nó final de um novo grafo.

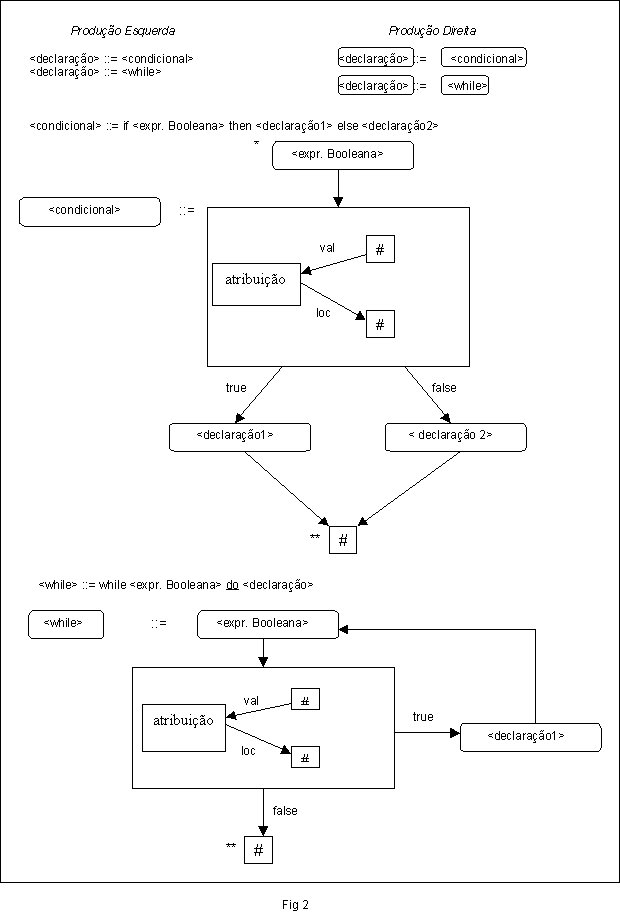
A figura 2 esclarece os conceitos de gramáticas pares e grafos de gramáticas e também serve para introduzir a notação.  Considerando as produções do while e expressão condicional acima, as produções à esquerda e à direita são apresentadas sob a seguinte notação: não terminais são palavras inclusas em “< . . . >” e o símbolo “::=” separa duas partes de uma produção ( necessário devido ao uso de “®” em H-grafos).  Nós não terminais têm o formato oval, enquanto nós terminais são representados por retângulos.  Os nós inicial e finais em cada produção de gramáticas de grafo são marcados por “*” e “**”, respectivamente.

2.2.2.  NÓs Rotulados e H-Grafos Reduzidos

            Uma simples técnica nos permite fazer as conecções necessárias.  Nós permitimos que os nós terminais nos H-grafos gerados por uma gramática de grafos sejam rotulados com um identificador.  Tipicamente muitos nós em um H-grafo gerado por uma gramática par terá o mesmo rótulo.  No H-grafo terminal da tradução de um programa, todos os nós com o mesmo rótulo são unidos em um único nó, deixando assim todos os arcos que eram ligados a qualquer um dos nós originais, ligados a um novo nó composto resultante.  É atribuído a este nó composto o valor nulo “ # “ ou qualquer outro valor não nulo.

            A regra de unir todos os nós com rótulos idênticos é chamada de regra de redução básica e os H-grafos resultantes são chamados de H-grafos reduzidos.  Muitas vezes unindo esses nós tornamos o nó resultante em um nó global.

2.3. AutÔmato H-Grafo

            Os H-grafos reduzidos resultantes do “tradutor” de uma Gramática Par representam programas “executáveis”. A execução é definida em termos de um autômato H-grafo  capaz de seguir um caminho através do grafo de um programa  e executar as operações encontradas ao longo do caminho.  Ordinariamente a figura de um autômato aparece em nossa mente como uma fita, uma posição inicial e estado interno, junto com uma função de transição que define como um autômato deve mover através de uma seqüência de estados, onde cada estado consiste de uma tripla: conteúdo da fita, posição inicial e estado interno.  No nosso autômato H-grafo, cada estado é representado por um H-grafo.  O autômato H-grafo começa em um estado inicial que consiste de um H-grafo reduzido como a saída de uma Gramática Par.  O autômato move através de uma seqüência de estados, cada um representando a execução de uma operação primitiva do programa original.  Em último lugar o autômato pode parar.  Se isto acontecer o estado final representa o resultado da execução do programa original.

Def 2.3.1 : Um autômato H-grafo B é um quíntupla B = ( N, A, S, S₀, d ), onde:

·        N é o universo de nós

·        A é um conjunto de átomos

·        S é um conjunto de estados ( um conjunto de H-grafos sobre N e A )

·        S₀  Í S  é o conjunto de estados iniciais

·        d: S ® S  é a função de transição

d é definida em termos de:

(1)   uma instrução-buscar-e-executar (um ciclo de dois passos)

(2)   um conjunto de esquemas de instruções primitivas, cada um definido como uma transformação de H-grafo estritamente local.

4- ConclusÃo

 Com a utilização dos conceitos de gramáticas formais e autômatos para  dominar os conceitos de estruturas H-grafos e linguagens de programação, o objetivo deste documento é encontrar uma teoria formal satisfatória que permita a definição e análise de Linguagens de Programação reais através de ferramentas matemáticas desenvolvidas para um trabalho mais teórico em gramáticas formais e autômatos. 

Com este conhecimento de H-grafos, Gramáticas Pares e Autômatos de H-grafos, temos uma visão mais nítida das linguagens de programação.