MÁQUINAS DE ESTADOS  X  PETRI NET

        Talvez um dos maiores impulsos que tenha levado Petri a este tema em sua tese de doutorado tenha sido a insuficiência com a qual os autômatos tratavam o caso de processos concorrentes e paralelos . Se observarmos bem o diagrama de estados apresentado à esquerda  , a sua característica principal é a  decisão em qual dos seguintes estados deve-se prosseguir ou não . Como podemos perceber nesta figura , o estado 1  toma a decisão de ir para o estado 2 ou de ir para o estado 4 , e nunca para os dois paralelamente . O mesmo acontece com outros estados e a suas recpectivas decisões do caminho a seguir . Já as  RdP´s ( figura da direita) além de garantirem o poder de decisão , também nos dá o poder do uso do paralelismo , como podemos logo verificar pela figura correspondente .

       Para transformarmos uma máquina de estado em uma RdP equivalente , associa-se a cada estado da máquina um lugar na rede e cada arco da máquina uma transição na rede . Cada arco da máquina de estado representa uma mudança de estado , portanto o estado atual ( representado na rede por um lugar ) é a pré-condição da transição ( rede ) que representa a mudança de estado . O próximo estado é a pós-condição dessa transição .A mudança de estado , bem como o próximo estado atingido , depende tanto do estado atual quanto das entradas do sistema . Dessa forma , se representarmos as entradas através da associação de condições externas às transições , veremos que cada transição da rede terá apenas um lugar de entrada e apenas um lugar de saída . Como sabemos , é possível representar as entradas e saídas através de lugares , assim como os estados da máquina . O lugar que representa o estado atual é marcado enquanto os demais não estão marcados .

        Agora iremos apresentar uma máquina de estados que representa um sistema que detecta uma seqüência de dois ou mais símbolos 0 de um alfabeto . Representamos o alfabeto de entrada como Ai = { 0,1 } . O estado inicial da máquina é o A . Se um caracter 1 chegar à entrada , a máquina continuará no estado A e a saída será zero . Caso chegue à entrada um caracter 0 , a máquina vai para o estado B e a saída continua em zero . Caso a máquina esteja no estado B , e chegue à entrada um caracter 0 , máquina continuará neste estado e a saída irá para 1, indicando a seqüência de dois ou mais caracteres 0´s . No entanto , se a máquina estiver no estado B e chegar à entrada um caracter 1 , a máquina retorna ao estado A e a saída será 0 ( veja figura abaixo ) .

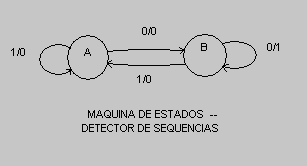
        Na figura abaixo , apresentamos a rede correspondente a esta máquina , ou seja , uma rede que detecta a chegada de dois ou mais símbolos 0 colocando a saída em 1 . Caso contrário , a saída permanece em 0. Embora a representação por RdP´s das máquinas de estado seja menos compreensível , as RdP´s possibilitam a composição seqüencial e paralela de redes para a construção de modelos mais complexos , através da fusão de lugares de entrada e saída .

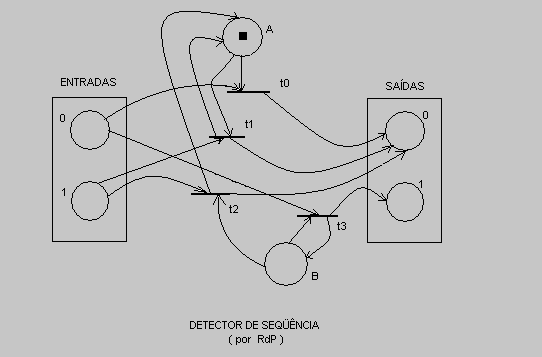
        Na verdade as máquinas de estado são uma subclasse das redes de Petri , caracterizando-se por restrições ao número de arcos que podem ser entrada e saída de uma transição .Cada transição da rede só pode ter um arco como entrada e um arco como saída .