Ramificações e Agrupamentos

Muitas formas biológicas são "ramificadas", "fragmentadas", ou "celular" em aparência e crescimento. Para permitir que ramificações ocorram nas interpretação de gráficos tartaruga, nós utilizamos símbolos [("push")] e ] ("pop") para permitir que a tartaruga siga a ramificação a cada vez e depois voltar a posição que se começou a ramificar. Nós começaremos com uma ramificação simples onde um tronco principal gera uma ramificação de apenas um lado.

Angle 10
Axiom F
F=F[+F]F

Isso pode ser visto como uma substituição de cada aresta pela seguinte configuração:

Figura 12: Ramificação Simples

A mudança de ângulo e um passo é conseguido com os operadores pop e push. Escalonando de tal forma que o tronco principal permanece do mesmo tamanho, nós vemos a sequência de gerações na figura abaixo.

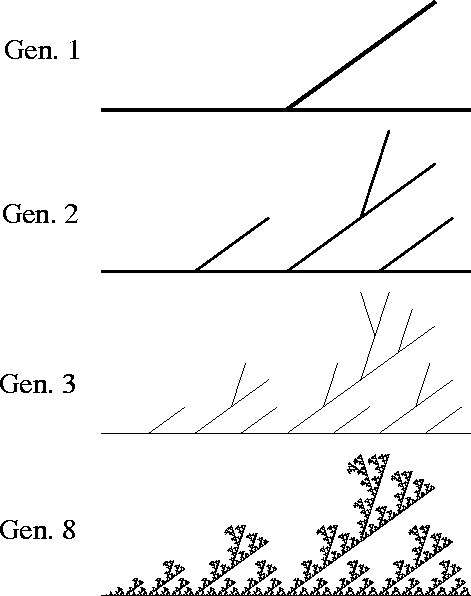
Figura 13: Gerações de Ramificações

Mesmo com esse simples L-system, pode-se visualizar um ramo de um arbustro ramificando-se recursivamente. Notavelmente, muitas imagens realísticas dos desenvolvimentos biológicos podem ser modelados pelos L-systems que não são muito complicados.

Para finalizar essa seção, nós mostramos uma figura de um sistema "BUSH ". O modelo é uma ramificação simples, levemente assimétrico e com ramificações levemente encurvadas .

Angle 16
Axiom ++++F
F=FF-[-F+F+F]+[+F-F-F]

O ângulo  permite um encurvamento suave. O tronco principal existe somente antes da ramificação, não depois. Os quatros +´s no axioma orientam a estrutura verticalmente. A geração 5 está nesta figura.
 

Figura: L-system arbusto, geração 5

A medida que nós passamos para gerações mais avançadas, os galhos do bush sistema agrupam-se numa maneira que dá uma aparência tri-dimensional para o arbustro. L-systems tri-dimensional verdadeiros podem ser construídos trocando-se + e - por um conjunto de seis rotações tri-dimensionais, um par para cada eixo de rotação entre os eixos x, y e z.