L-systems famosos da história da matemática
Um dos grandes temas da matemática do século dezenove
foi o esforço coletivo de muitos matemáticos em colocar os
métodos do cálculo e análise numa fundamentação
rigorosa. A epidemia de estudantes modernos de cálculo, a 
- 
definição
de limites, é um dos grandes sinais deste esforço. Com novas
idéias poderosas sobre a noção exata de "limite" e
"continuidade", os matemáticos foram pelo menos capazes de explorar
inteiramente novos tipos de objetos geométricos.
Um estudo pioneiro da natureza dos conjuntos e dos números reais foi tentada pôr George Cantor na última metade do século dezenove. Embora a idéia de números reais como expansão decimal tenham existido pôr algum tempo antes de Cantor, Cantor foi o primeiro a realizar algumas das surpreendentes implicações apresentadas põe esta idéia .Talvez o seu mais famoso argumento é a simples observação que dada qualquer enumeração dos números reais na forma decimal, digamos:
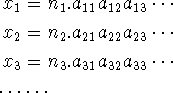
onde cada 
é um inteiro e cada 
é um dígito de 0 a 9,nos podemos sempre encontrar um número
real 
que não esteja na lista escolhendo 
para ser um dígito diferente de 
(e 9, para evitar números que terminam todos eml 9's). Este argumento
da diagonal prova que o conjunto dos números reais são incontáveis.
Isto foi no momento um amargo e aborrecido para os filósofos aceitarem
que existiam números irracionais; O argumento de Cantor mostra muito
mais. De certa forma, a grande maioria dos números não
são racionais, nem mesmo algébrico (soluções
equações polinomiais com coeficientes racionais).
Esta mudança na filosofia matemática, embora isto pareça quase desprovido de controvérsia hoje, é similar a transformação que tem tido lugar na dinâmica através das últimas décadas. O limite geométrico e dinâmico é como um fractal ou uma natureza caótica.
A manipulação das expansões decimais reflete a percepção da expansão dos dígitos como um sistema simbólico dinâmico .Os estados simbólicos são simplesmente os dígitos 0 até 9. Uma expansão decimal é uma listagem dos estados através de cada geração; o número propriamente é o comportamento do sistema dinâmico. Esta idéia sugere todos os tipos de coisas curiosas a considerar. Cantor formulou um particularmente um interessante conjunto baseado na restrição a "sistemas simbólicos dinâmicos" das expansões dos dígitos. Nós precisamos fazer uma pequena variação da nosso sistema de expansão. Uma vez que exista nada sobre o uso da base 10, nós podemos também trabalhar com expansões em outras bases, particularmente a base 3. Na base 3,existem exatamente três dígitos 0,1, e 2. Uma expansão de um número (chamada expansão ternária) tem a forma usual
onde cada dígito é 0,1, ou 2. O número atual é composto de potências de 3 (ao invés de potências de 10) como as séries:
Cantor definiu um conjunto C para consistir de todos números com a expansão ternária que usava somente 0's e 2's mas não 1's.Uma expansão terminada toda com 2 é permitida em C. O argumento da diagonal pode ser usado para mostrar que C é novamente incontável, e portanto neste senso ele tem uma grande quantidade de pontos.
Para representar o conjunto de Cantor, nós devemos considerar
somente os pontos do intervalo unitário [0,1].Considerando o primeiro
dígito, pontos começando com 
não ocorrem em C, com duas exceções . O limite de 
e 
tem pelo menos
uma possível expansão em todos 0's e 2's ebentão pertence
a C. Assim, na tentativa destrinchar C, nós devemos primeiro cortar
fora a terceira parte do meio do ntervalo (1/3,2/3).Quando nos consideramos
o segundo dígito, nós devemos também eliminar expansões
começando em 
e 
. Estes correspondem as
terceiras partes dos intervalos restantes (1/9,2/9) e (7/9,8/9). Este processo
de cortar a terceira parte do meio continua indefinidamente .O resíduo
que sobrar e o conjunto de Cantor.
Daí surge que este processo pode ser escrito como um L-system bem simples (chamado de CantorDust no FRACTINT):
Axiom F
F=FGF
G=GGG
O ângulo é irrelevante neste caso. Nós começamos
com um segmento de reta F e o substituímos por um modelo
de desenhar um passo, mover um segundo passo, e desenhar o terceiro passo.
Isto conduz a esculpir a terceira metade. A seqüência
de gerações é mostrada abaixo.
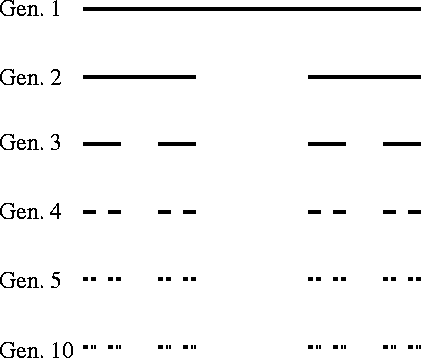
Figura 15: Gerações do L-system de Cantor
O limite é impreciso; ainda , este tipo de distribuição aparece na natureza, por exemplo, a distribuição da matéria do universo. Mandelbrot chama iste tipo de objeto fractal geométrico de poeira.
Desde Euclides, as distinções entre pontos, retas e planos tem parecido intuitivamente claro. Com a descrição do conjunto de Cantor, Cantor levantou uma nuvem de poeira que foi nem como um ponto ou nem como uma reta. Depois Cantor se voltou sua atenção para a diferença entre uma reta um plano. Por vinte anos Cantor tentou provar que existiam de alguma forma mais pontos no plano do que numa reta. Isto foi um choque para ele mesmo e para o mundo descobrir que isso era falso. A verdade vem novamente de uma aproximação dinâmica simbólica. Qualquer par de expansões de dígitos
pode ser tratada junto para formar uma única expansão
e reciprocamente qualquer expansão de dígitos pode ser tratada como um par de expansão de dígitos. Esta idéia (com um pouco de elaboração ) prova que os pontos em e podem ser colocados em uma correspondência bionívoca. Cantor já tinha aceito a idéia de "correspondência bionívuca" como significado para decidir quando dois conjuntos infinitos tem o mesmo número de elementos.
Esta função entre 
e 
é muito artificial no sentido de que pontos que estavam próximos
um do outro em
podem ser tratados como dois pontos em
que não estão próximos um do outro. Isto é,
dizemos que a correspondência de Cantor não é continua.
Uma pergunta continuou se ou não existe um uma função 
que satisfaça todas as seguintes condições:
então 
.
podem ser expressos como f(x) para algum ponto x em
.# f é contínua (na notação do cálculo, isto deve ser escrito
é contínua.Isto foi largamente acreditado que era impossível, até
o mundo esta novamente chocado pela descoberta de Peano da função 
que é contínua e sobrejetora! Uma função continua
de um intervalo unitário no plano é geralmente pensado como
uma curva. Assim, o exemplo de Peano é conhecido como um preenchimento
de uma região (área) ou preenchimento do espaço curva.
Construções parecidas podem produzir curvas que preenchem
qualquer cubo de dimensão finita 
.
A idéia é de natureza dinâmica; A construção
de Peano pode ser empreendida por um L-system, e os três exemplos
Peano1-3 no FRACTINT são variações da construção.
Nós podemos discutir a versão original
Peano1 { ; Adrian Mariano
; from The Fractal Geometry of Nature by Mandelbrot
Angle 4
Axiom F-F-F-F
F=F-F+F+F+F-F-F-F+F
}
A configuração inicial é um quadrado. Nós
podemos pensar da primeira geração da nossa função 
como mapeando um intervalo unitário como implicando como possível
neste quadrado, em particular, 
é lado de baixo, 
é o lado direito, 
é lado de cima, e
é o lado esquerdo.
Cada lado da configuração anterior é substituído
por nove segmentos do gerador (produção) da figura abaixo.
Esta figura também mostra o caminho da curva pelo contorno das pontas.
O quarto intervalo que foi mapeado no segmento original pode agora ser
dividido em nove subintervalos iguais, e cada um dos nove é mapeado
no modo mais simples para o correspodente segmento na geração
do modelo. Todos estes segmentos juntos dão uma segunda função
contínua 
. Continuando este processo, nós obtemos uma seqüência
de funções contínuas 
que convergem uniformemente para uma função contínua 
. A imagem da função limite é um quadrado sólido.
A segunda geração é mostrada na figura abaixo.Sem
fazer os caminhos claros, as imagens das outras gerações
não são muito informativas.
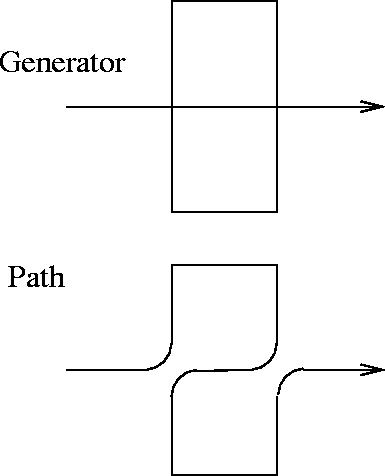
Figura 16: regra de produção de Peano
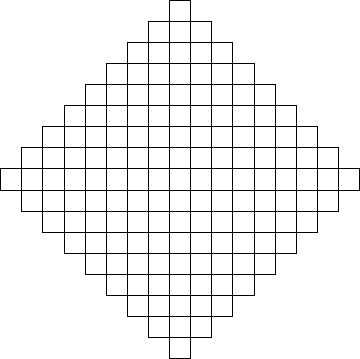
Figura 17: Segunda geração da curva de Peano
Com a descoberta das curvas de Peano, a pergunta de se existe ou não
uma função
satisfazendo as 1-4 acima (tal função é chamada homomorfismo)
se tornou mais precária. A resposta final de que é impossível
foi dada por Brouwer no início do século vinte e é
baseada em alguns matemáticos que finalmente estabeleceram a noção
rigorosa de dimensão topológica.
