Similaridade Própria dos L-systems
Pare um pouco e reveja algumas das figuras surgidas dos L-systems que nós consideramos. O objeto geométrico limitante é um exemplo do que geralmente nós chamamos, na teoria de sistemas dinâmicos, de indutor. Geralmente, isso significa alguma situação física na qual o sistema de alguma forma converge. Para alguns sistemas dinâmicos simbólicos, os indutores são sequências infinitas produzidas. Para os L-system derivados dos gráficos tartaruga, o indutor é a curva ou forma limite. Para chegar-se a forma final, nós devemos reescalonar as gerações tal que o "tamanho do passo" d é decrementado de um fator apropriado de geração para geração.
Quando nós vemos a forma final (ou aproximada), a evolução e o reescalonamento são muitas vezes visualmente aparentes. Considere a primeira Curva do Dragão. Nessa figura, nós mostramos como as formas finais podem ser divididas em duas figuras congruentes.
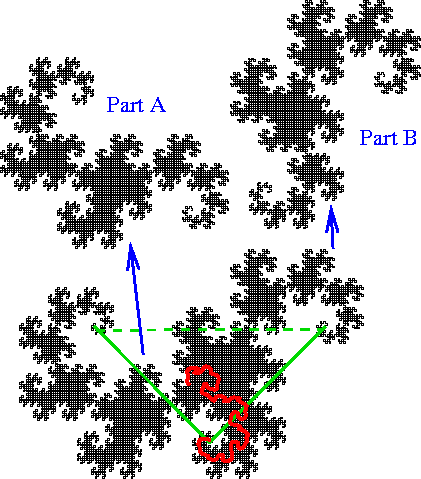
Figura 18: Dividindo o dragão: As duas metades do dragão abaixo são marcados como partes A e B. A divisão é marcado em vermelho.
O triângulo retângulo isósceles original é
marcado em verde na figura. As duas metades menores são cada uma
construída em um segmento de comprimento 
vezes maior que o dragão original. Como as duas metades são
congruentes, uma metade deve encaixar exatamente no topo de outra metade
depois de uma translação e uma rotação
de 
.
Nós vemos que o dragão fractal é composto de dois
pedaços congruentes, cada um é escalonado por
do dragão original. Esse é um exemplo de similaridade própria:
similaridade de um objeto inteiro com seus pedaços menores.
Para muitos L-systems gráficos listados no FRACTINT e em
outros locais, nós podemos associar dois números : um "número
de pedaços congruentes" que exprime o número de partes em
que se pode dividir um L-system, e um "fator de escalonamento" que mede
cada parte proporcionalmente ao objeto original. Para o dragão fractal,
o número de pedaços é 2 e o fator de escalonamento
é 
.
Esses números podem ser parcialmente deduzidos pelas regras dos
L-systems, embora um método universal para se fazer isso não
seja conhecido. Para o dragão, nós vemos nas regras de produção
do L-system que cada segmento reproduz dois pedaços menores de tamanho
menor que o original.
Como um segundo exemplo, considere a curva de Koch, o qual nós mostramos abaixo dividida em partes similares. A regra de produção converte cada segmento em 4 novos segmentos de comprimento igual a 1/3 do original. Portanto, não é surpresa ver quatro pedaços similares, cada um com um terço do tamanho da curva de Koch original.
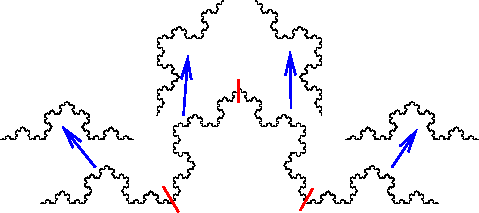
Figura 19: Dividindo a curva Koch.
Similaridade própria é um conceito chave na teoria de
sistemas dinâmicos e da geometria fractal resultante.
