INTRODUÇÃO

    O conceito de redes de Petri foi introduzido por Carl Adam Petri , em sua tese de doutoramento intitulada Kommunikation mit Automaten (1962) na faculdade de Matemática e Física da Universidade de Darmstadt na então Alemanha Ocidental . Nos anos seguintes, a medida que seu trabalho foi sendo introduzido em outros países, esse conceito difundiu-se e vem sendo aperfeiçoado através da promoção de workshops, conferências internacionais e publicações de novos trabalhos, os quais vêm formando mestres e doutores nessa área .

    Redes de Petri são uma ferramenta gráfica e matemática de modelagem (descrição/especificação) que podem ser aplicadas em diversos tipos de sistemas apresentando um bom nível de abstração em comparação com outros modelos gráficos . Além disso , as Redes de Petri ( RdP´s ) possibilitam a verificação da corretude do sistema especificado . Usando-se  RdP , pode-se modelar sistemas paralelos , concorrentes , assíncronos e não-determinísticos .  

    Sendo um modelo do tipo estado-evento, onde cada evento possui pré-condições que vão permitir sua ocorrência e pós-condições decorrentes desta , as quais são por sua vez pré-condições de outros eventos posteriores , como veremos mais adiante . Áreas como: redes de computadores e protocolos de comunicação, sistemas operacionais, programação paralela, bancos de dados distribuídos e sistemas flexíveis de manufatura , enfim, qualquer área em que a concorrência seja um fator preponderante, são passíveis de ter vantajosamente aplicadas as redes de Petri . Outra característica importante, é que ela permite a análise da estrutura e do comportamento dinâmico do sistema modelado, e tais informações são obtidas da mesma representação.

    Todo o formalismo matemático das redes de Petri possibilita a análise precisa do modelo; verificações de propriedades inerentes aos sitemas concorrentes, tais como relações de precedência entre eventos, sincronização e (in)existência de bloqueio são feitas formalmente . Além de todas estas vantagens , permite a visualização dos processos e a comunicação entre eles .

    As  RdP´s são formadas por dois tipos de componentes : um ativo denominado de transição e outro passivo denominado lugar . Os lugares correspodem às variáveis de estado e as transições às ações ( eventos ) realizadas pelo sistema . Estes dois elementos são os vértices do grafo associado às RdP´s . Os arcos que interligam lugares às transições correspodem à relação entre as condições verdadeiras , que em um dado momento , possibilitam a execução das ações , enquanto os arcos que interligam transições aos lugares representam a relação entre as ações e as condições que se tornam verdadeiras com a execução das ações . Uma RdP pode ser vista como um grafo orientado mais uma marcação , definida por :

• LUGAR ( representado por um círculo ) : que modela condição ou estado de um agente (componente de hardware ou software) e que corresponde às condições que devem ser certificadas para os eventos acontecerem ;
• TRANSIÇÃO ( representada como um retângulo ou barra ) : que modela um evento, tal como o início de uma operação que corresponde aos eventos que caracterizam as mudanças de estado do sistema ;
• ARCO ORIENTADO : que interliga um lugar a uma trasição ou vice-versa, encadeando condições e eventos - os lugares e as transições são interligados por arcos direcionados ponderados* .
• MARCA OU FICHA : representa um recurso disponível ao agente , o posicionamento dessas fichas em alguns lugares do grafo , constitui a marcação . A evolução da marcação permite modelar o comportamento dinâmico do sistema .

    Vejamos esses conceitos ilustrados na figura abaixo:

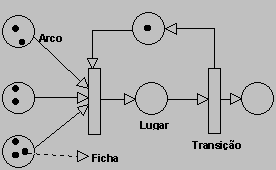
        A Rede de Petri é, portanto, um formalismo que permite a modelagem de sistemas dinâmicos discretos com grande poder de expressividade, permitindo representar com facilidade todas as relações de causalidade entre processos em situações de: seqüencialidade , conflito, concorrência e a sincronização. O interesse pelas redes de Petri tem aumentado, nos últimos anos, devido às possibilidades representadas pelas redes de alto nível, que permitem modelar sistemas com um nível de complexidade maior, por gerarem modelos mais compactos; e pelas extensões que incorporam parâmetros temporais .

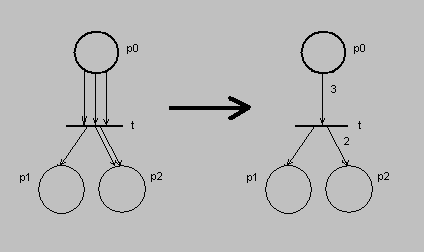
         * Os vértices de um grafo associada a uma RdP podem ser interligados por múltiplos arcos . Por exemplo , um lugar pode ser conectado a uma transição através de diversos arcos ou vice-versa . Por conveniência , podemos substituir os múltiplos arcos por um único arco valorado , onde o numeral associado ao arco corresponde ao número de arcos que interligam os vértices ( veja figura abaixo ) .