Projeto de Sistemas Integrados de HW/SW com Gerência de Processo
Jones Albuquerque
 Departamento de Ciências Exatas
Departamento de Ciências Exatas
DEX - UFLA. Caixa Postal 37.
37200-000. Lavras, MG - BRAZIL
Phone/Fax: +55 35 829-1371
jones@ufla.br, joa@dcc.ufmg.br
Claudionor Coelho Jr.
Departamento de Ciência da Computação
DCC - ICEx - UFMG. Caixa Postal 702.
30161-970. Belo Horizonte, MG - BRAZIL
Phone: +55 31 499-5860 Fax: +55 31 499-5858
coelho@dcc.ufmg.br
Resumo:
Este texto descreve uma proposta de metodologia para o projeto de
sistemas integrados de hardware (HW) e software (SW) considerando aspectos
de qualidade do processo de desenvolvimento. Fatores como alocação de
times; gerência de riscos e análise de incerteza, todos presentes no
projeto de sistemas HW/SW, não são tratados pelas metodologias correntes.
Palavras-chave: HW/SW codesign, programação linear estocástica, gerenciamento de times de desenvolvimento.
O interesse em sistemas de computação compostos de componentes de hardware e software tem se tornado crescente por razões de flexibilidade, complexidade dos sistemas, otimização do custo e redução de time-to-market. A disponibilidade de ambientes de projeto suportando desde a especificação até a prototipação de sistemas digitais complexos tem permitido o projeto de diversas aplicações, cada vez mais complexas: equipamentos médicos, controle de processo, aviação, telefonia e telecomunicações, entre outros.
Esta complexidade dos sistemas de computação cada vez mais exige garantia de qualidade do processo de desenvolvimento, não permitindo mais um gerenciamento de atividades sem metodologia adequada. Na Engenharia de Software tais metodologias já estão em nível comercial, e.g., CMM [26] e PSP [14,15], apesar de ainda possuírem algumas restrições [5,6,16]. Em sistemas integrados de hardware e software ainda há muito a se fazer nesta direção. Começam a surgir, nesta área, os primeiros grupos de discussões nesta direção [29].
A metodologia de HW/SW Codesign é a mais comumente utilizada para suportar o projeto de sistemas compostos de hardware e software. Esta metodologia é composta por quatro atividades principais, ilustradas na Figura 1 e descritas a seguir:
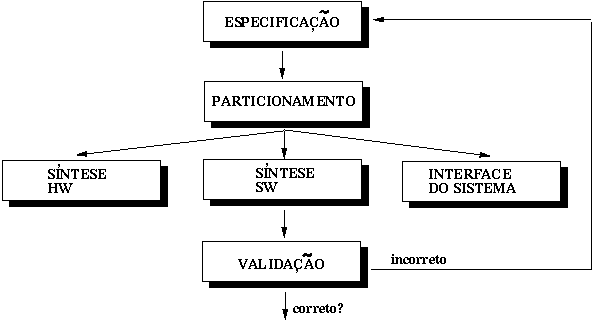
Figure 1: Fluxo de atividades da metodologia de HW/SW Codesign [17].
- Especificação e análise. Nesta etapa, as principais características do sistema são definidas com base nas especificações do cliente/usuário, então o sistema é descrito usando linguagens visuais e/ou textuais de acordo com o nível de abstração desejado;
- Particionamento é a tarefa responsável pela decisão de quais partes da especificação serão implementadas em hardware e quais serão implementadas em software;
- Síntese envolve implementar as componentes hardware e software nas tecnologias específicas, e.g., portas lógicas para hardware e linguagem de máquina para software;
- Validação visa garantir que o sistema resultante e a especificação são semanticamente equivalentes. Existem diferentes técnicas disponíveis para validar um sistema variando de especificação formal a simulação e emulação [1,23].
Acreditamos que a incorporação de tratamento de riscos a estas etapas de projeto é uma maneira de buscar a qualidade de processo tão desejada no desenvolvimento de sistemas integrados de hardware e software.
Mostraremos neste trabalho que, especificamente, incorporando à fase de particionamento as questões de risco e times de desenvolvimemto anteriormente mencionadas, estamos tornando mais realista o planejamento de atividades de projeto e conseqüentemente melhor atendendo às restrições de projeto como time-to-market, custos, entre outras.
Tradicionalmente [9,18,1] as metodologias para o projeto integrado de sistemas HW/SW tratam as questões do desenvolvimento de sistemas de maneira simplificada quando se referem ao processo de desenvolvimento. Consideram como se o sistema fosse desenvolvido por um único indivíduo, não considerando aspectos que envolvem times de desenvolvimento (gerenciamento e alocação), habilidades individuais, desenvolvimento concorrente de partes do projeto, nem análise de risco para time-to-market.
O tratamento de riscos no projeto de sistemas integrados de hardware e software não é uma idéia inovadora [13,19,10]. Contudo, a literatura apresenta metodologias completamente voltadas ao produto e não incorporam nenhum tratamento para as restrições do processo de desenvolvimento. Estratégias nesta direção são bastante comuns na Engenharia de Software [21,20].
A nossa metodologia visa exatamente preencher esta lacuna deixada por outras metodologias de projeto de sistemas HW/SW. Temos conseguido alguns progressos nesta direção [2,3,4]. Por outro lado, o que apresentaremos a seguir são as nossas perspectivas para a nossa metodologia, pois a mesma ainda não está totalmente validada.
Nossa metodologia é aplicada às fases iniciais do projeto de um sistema, quando ainda poucas informações são conhecidas. Assim, o que desejamos é retratar no processo de desenvolvimento quão poucas são estas informações, isso através de estimativas dos membros do time de desenvolvimento.
Com o objetivo de tornar mais clara a nossa proposta, descrevemos a seguir a seqüência de atividades durante o desenvolvimento de um sistema. Assumimos que cada time de desenvolvimento detém o conhecimento de uma tecnologia específica e que as estimativas são dadas com base nos dados históricos do time de desenvolvimento, coletados em projetos passados via metodologias como CMM e PSP. Partimos de uma especificação com parâmetros e restrições, e executamos os seguintes passos:
- Primeiro, o gerente de projeto deve estar de posse da especificação do sistema e deve dividi-la em tarefas;
- Cada gerente de time de desenvolvimento expressa suas estimativas (e.g., time-to-market, custo monetário, tempo de execução, etc) para cada tarefa da especificação considerando as tecnologias e as habilidades dos times que dispõe;
- De posse das estimativas dos times de desenvolvimento, o gerente de projeto construirá o grafo de tarefas [7] mostrando todas as dependências, tanto de implementação como de desenvolvimento. Com este grafo e com as retrições do sistema é possível modelar o particionamento do sistema como um problema de programação linear estocástica binária, descrito na Seção Formulação, neste texto;
- DO {
- Particiona-se o sistema considerando o grau de confidência presente nas estimativas dos times de desenvolvimento;
- O gerente de projeto escolhe quais tarefas estão mais aptas a serem implementadas, tornando maior o grau de confidência destas tarefas e, conseqüentemente, modificando os parâmetros do particionamento;
} WHILE (todas as restrições não tenham sido satisfeitas OR todas as tarefas não estejam com graus de confidência satisfatórios).
O último passo da metodologia é um laço e só termina quando todas as restrições estão satisfeitas e todas as tarefas estejam definidas com um grau de certeza que garanta as restrições.
Assim, quanto mais precisos forem os parâmetros (maiores graus de confidência), melhor será a solução do particionador. Entretanto, a cada solução temos o risco associado à solução em qualquer estágio do desenvolvimento.
As estimativas dos times de desenvolvimento podem ser classificadas em dois tipos: estimativas de desenvolvimento e estimativas de implementação. Estimativas de desenvolvimento são geralmente relacionadas às habilidades dos times para executar ou implementar uma determinada tarefa. Elas são geralmente medidas em tempos de desenvolvimento dos times, carga dos times e riscos de implementação. Estimativas de implementação estão relacionadas com métricas de produção tais como tempo de execução ou consumo de energia.
Uma estimativa pode ser representada por uma 3-upla 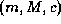 , onde m é o valor mínimo, M o máximo e c o grau de confidência do intervalo
, onde m é o valor mínimo, M o máximo e c o grau de confidência do intervalo 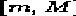 , por exemplo, (``muito alto'', ``alto'', ou ``baixo''). Estes graus de confidência mudam de acordo com o projeto e são baseados em dados históricos; se o time tem dados históricos precisos de suas tarefas realizadas e de grande relação com a estimativa então seu grau é ``muito alto'' e se ele não possui dados históricos ou se os dados não têm relação com a estimativa então seu grau é ``baixo''. Estes dados históricos podem ser coletados por monitoração de tempo, esforço e estimativas de projetos passados. Desta forma, tem-se um completo perfil do time de desenvolvimento. [14,26] apresentam métodos para obter os dados históricos e avaliar quão precisos eles são (graus de confidência).
, por exemplo, (``muito alto'', ``alto'', ou ``baixo''). Estes graus de confidência mudam de acordo com o projeto e são baseados em dados históricos; se o time tem dados históricos precisos de suas tarefas realizadas e de grande relação com a estimativa então seu grau é ``muito alto'' e se ele não possui dados históricos ou se os dados não têm relação com a estimativa então seu grau é ``baixo''. Estes dados históricos podem ser coletados por monitoração de tempo, esforço e estimativas de projetos passados. Desta forma, tem-se um completo perfil do time de desenvolvimento. [14,26] apresentam métodos para obter os dados históricos e avaliar quão precisos eles são (graus de confidência).
Tratamos as estimativas de modo probabilístico, pois os valores reais só são obtidos quando a tarefa é implementada. Baseamos nosso tratamento probabilístico na Distribuição Normal (ou Gaussiana), dada pela função de distribuição de probabilidade
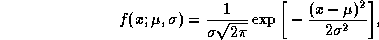
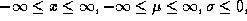
onde  é a média e
é a média e  o desvio padrão definido pelos graus de confidência.
o desvio padrão definido pelos graus de confidência.
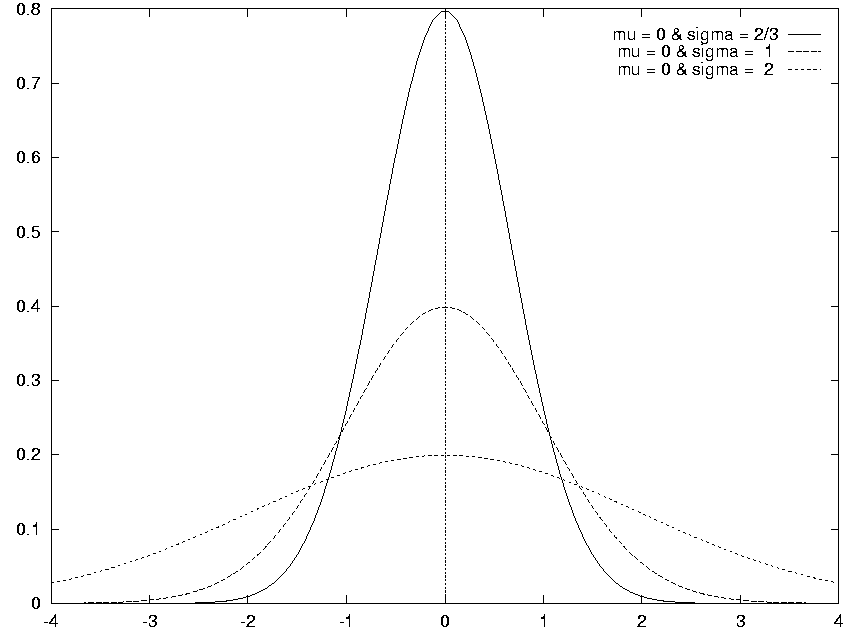
Figure 2: Distribuições Normais para um mesmo intervalo e mesma média (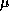 ) e diferentes graus de confidência (
) e diferentes graus de confidência (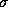 ).
).
A Distribuição Normal foi escolhida porque é o melhor modelo estatístico para casos de propósito geral na engenharia [12] e é uma boa representação para estimativas humanas em geral [27]. Embora [28] tenha mostrado que as distribuições Rayleigh e Gamma representam curva de carga de trabalho (homens-hora) em projetos melhor que qualquer outra curva, também mostrou algumas limitações para estas curvas. A escolha da forma Normal também foi motivada por sua simplicidade e por uma estratégia de aproximação apresentada na literatura e também usada neste trabalho, chamada ``aproximação por valor esperado'' [24].

*[1.3ex]
Tabela 1: Definição de 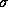 .
.
A Distribuição Gaussiana está associada com a 3-upla 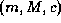 de forma que
de forma que 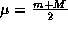 and
and 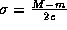 . A Tabela 1 apresenta os graus de confidência para valores inteiros de c, i.e., c=3 (``Muito Alto''), c=2 (``Alto'') e c=1 (``Baixo''). Os graus de confidência representam a possibilidade de uma estimativa estar no intervalo [m,M]. Na Figura 2, se tomarmos m=-2 e M=2, podemos comparar os diferentes graus de confidência associados com estes valores: Muito Alto para a curva mais interna (
. A Tabela 1 apresenta os graus de confidência para valores inteiros de c, i.e., c=3 (``Muito Alto''), c=2 (``Alto'') e c=1 (``Baixo''). Os graus de confidência representam a possibilidade de uma estimativa estar no intervalo [m,M]. Na Figura 2, se tomarmos m=-2 e M=2, podemos comparar os diferentes graus de confidência associados com estes valores: Muito Alto para a curva mais interna (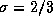 ), Alto para a curva do meio (
), Alto para a curva do meio (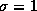 ) e Baixo para a curva mais externa (
) e Baixo para a curva mais externa (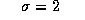 ).
).
Com esta abordagem, podemos representar as incertezas e estimar as capacidades e habilidades dos times de desenvolvimento.
O particionamento HW/SW pode ser formulado num problema de programação linear estocástica [11,8] com restrições descritas por equações como
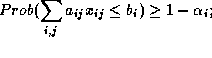
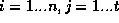 ,
, 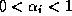 ,
,
onde 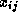 é uma variável binária e assume valor um (1) se a tarefa i é implementada pelo time j, n é o número de tarefas e t a quantidade de times dispoíveis,
é uma variável binária e assume valor um (1) se a tarefa i é implementada pelo time j, n é o número de tarefas e t a quantidade de times dispoíveis, 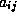 e
e 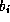 representam os parâmetros de restrição, e
representam os parâmetros de restrição, e 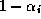 a probabilidade de certeza da restrição.
a probabilidade de certeza da restrição.
A função de custo pode ser definida como um somatório ponderado de restrições, onde restrições com maior relevância para o projeto tenham pesos maiores.
Resolver o particionamento HW/SW significa encontrar um mapeamento 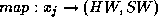 que satisfaça todas as restrições e minimize a função objetivo.
que satisfaça todas as restrições e minimize a função objetivo.
A formulação estocástica apresentada anteriormente e usada para resolver o particionamento não pode ser diretamente mapeada num problema ILP ( Integer Linear Programming) [30], os quais podem ser resolvidos por sistemas comerciais com número restrito de equações e variáveis. Daí a necessidade de uma aproximação por valor esperado  como em [22], onde a probabilidade da soma pode ser aproximada pela soma das probabilidades. Então as equações
como em [22], onde a probabilidade da soma pode ser aproximada pela soma das probabilidades. Então as equações
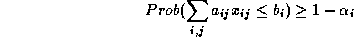
poderiam ser escritas em suas formas aproximadas como
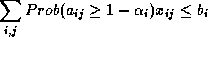
onde a incerteza (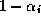 ) é transferida para os coeficientes
) é transferida para os coeficientes 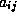 representando a caracterização dos graus de confidência apresentada anteriormente.
representando a caracterização dos graus de confidência apresentada anteriormente.
Com esta formulação podemos obter resultados interessantes, pois além do particionamento fornecemos o grau de certeza do resultado baseado nas estimativas dos times de desenvolvimento.
O aumento da complexidade computacional para resolver o problema de programação linear estocástica é compensado pela melhor qualidade das respostas obtidas.
Este texto apresentou uma metodologia para projeto de sistemas integrados de hardware e software. A principal contribuição deste trabalho é a incorporação nas restrições do sistema de parâmetros como fatores humanos, times de desenvolvimento, análise de risco e o tratamento da incerteza presente em qualquer atividade que envolva seres humanos.
Obviamente o esforço computacional para resolver o problema estocástico (aproximado neste trabalho para ILP), em comparação com outras metodologias, é bem maior. Contudo, como estamos trabalhando nos estágios iniciais do projeto, o número de variáveis a se considerar torna o problema computacionalmente viável como mostrado em [25]. Além disso, outros métodos para a resolução de problemas de programação linear estocástica têm aparecido na literatura [8], os quais podem tornar a metodologia apresentada mais eficiente.
Referências
- 1
-
J. Adams and D. Thomas.
The design of mixed hardware/software systems.
In ACM 33th DAC, Las Vegas, 1996.
- 2
-
J. Albuquerque and C. C. Jr.
A stochastic model for risk analysis in hardware/software codesign.
In XXI Congresso de Matemática Aplicada e Computacional,
Caxambu-MG, set 1998. SBMAC-Sociedade Brasileira de Matemática Aplicada e
Computacional.
- 3
-
J. Albuquerque, C. C. Jr., C. Cavalcanti, and A. Fernandes.
A system-level design model for hardware/software codesign.
Technical Report DCC 012/98, UFMG, nov 1998.
- 4
-
J. Albuquerque, C. C. Jr., C. F. Cavalcanti, D. C. da Silva Jr., and A. O.
Fernandes.
System-level partitioning with uncertainty.
In 7th International ACM/IEEE Workshop on Hardware/Software
Codesign - CODES'99, pages 198--202, Rome - Italy, may 1999.
- 5
-
J. Albuquerque and S. Meira.
Psp-joa: Processo pessoal de software - uma abordagem oriantada a
java.
Master's thesis, Departamento de Informática, Universidade
Federal de Pernambuco, Janeiro 1997.
- 6
-
J. Albuquerque, S. Meira, and C. C. Jr.
Practical limits of the psp model.
In Proceedings of the Symposium on Software Technology -
SoST'98., Buenos Aires, Argentina, sep 1998. 27th International Conference
of the Argentine Informatics and Operations Research Society (SADIO).
- 7
-
E. Barros and S. Cavalcante.
Introdução a hardware/software co-design.
In XVII Jornada de Atualização em Informática -
JAI, volume II, pages 163--224. SBC, 1998.
- 8
-
M. Biswal, N. Biswal, and D. Li.
Probabilistic linear programming problems with exponential random
variables: A technical note.
European Journal of Operational Research, (111):589--597, 1998.
- 9
-
R. Camposano and J. Wilberg.
Embedded system design.
Design Automation for Embedded Systems An International
Journal, 1(1-2):5--50, January 1996.
- 10
-
V. Catania, M. Malgeri, and M. Russo.
Applying fuzzy logic to codesign partitioning.
IEEE Micro, pages 62--70, May/June 1997.
- 11
-
M. Dell'Amico, F. Maffioli, and S. Martello, editors.
Annotated Bibliographies in Combinatorial Optimization.
John Wiley & Sons, 1997.
Chapter 9.
- 12
-
G. Hahn and S. Shapino.
Statistical Models in Engineering.
John Wiley & Sons, 1994.
- 13
-
D. Herrmann, J. Henkel, and R. Ernst.
An approach to the adaptation of estimated cost parameters in the
cosyma system.
In 2nd International ACM/IEEE Workshop on Hardware/Software
Codesign - CODES'94, 1994.
- 14
-
W. S. Humphrey.
A Discipline For Software Engineering.
Adison Wesley, 1995.
- 15
-
W. S. Humphrey.
Introduction to the Personal Software Process.
Adison Wesley, 1997.
- 16
-
P. M. Johnson and A. M. Disney.
The personal software process: A cautionary case study.
In IEEE Software. IEEE, November/December 1998.
- 17
-
C. J. N. C. Jr., D. C. da Silva Jr., and A. O. Fernandes.
Hardware-software codesign of embedded systems.
In XI Brazilian Symposium on Integrated Circuit Design, pages
2--8, Búzios - RJ, september 1998. IEEE Computer Society.
- 18
-
A. Kalavade.
System-level Codesign of Mixed Hardware-Software Systems.
PhD thesis, University of California, CA, September 1995.
- 19
-
I. Karkowski and R. Otten.
Uncertainties in hardware-software co-synthesis of embedded systems.
In Workshop on High Level Synthesis Algoritms, Tools and Design
(HILES), Stanford University, January 1996.
- 20
-
J. Karlsson and K. Ryan.
A cost-value approach for prioritizing requirements.
IEEE Software, 1997.
- 21
-
T. M. Khoshgoftaar, E. B. Allen, R. Halstead, G. P. Trio, and R. M. Flass.
Using process history to predict software quality.
In IEEE Computer. IEEE, April 1998.
- 22
-
K. Marti and P. Kall.
Stochastic programing: Numerical techniques and engineering
applications.
In 2nd Gamm/IFIP-Workshop on Stochastic Optimization, volume
423. Springer-Verlag, June 1995.
- 23
-
G. D. Micheli and M. Sami.
Hardware Software Co-Design.
Kluwer Academic Publishers, 1996.
- 24
-
G. Nemhauser, A. H. G. R. Kan, and M. J. Todd, editors.
Handbooks in Operations Research and Management Science:
Optimization, volume 1.
North-Holland, 1989.
Chapter 8.
- 25
-
R. Niemann and P. Marwedel.
Hardware/software partitioning using integer programming, 1996.
IEEE ED&TC'96.
- 26
-
M. Paulk, B. Curtis, M. Chrissis, and C. Weber.
Capability maturity model for software, version 1.1.
Technical Report CMU/SEI-93-TR24, SEI - Software Engineering
Institute, 1993.
- 27
-
J. Pearl.
Probabilistic Reasoning in Intelligent Systems: Networks of
Plausible Inference.
Morgan Kaufmann Publishers, 1988.
- 28
-
K. Pillai and V. S. Nair.
A model for software development effort and cost estimation.
IEEE Transactions on Software Engineering, 23(8):485--497,
August 1997.
- 29
-
J. Plantin and E. Stoy.
Aspects on system-level design.
In 7th International ACM/IEEE Workshop on Hardware/Software
Codesign - CODES'99, pages 209--210, Rome - Italy, may 1999.
Group Discussion Topic Summaries.
- 30
-
A. Schrijver.
Theory of Linear and Integer Programming.
John Wiley & Sons, 1986.
Projeto de Sistemas Integrados de HW/SW com Gerenciamento de Processo
This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -no_navigation -split 0 spg99_joa.tex.
The translation was initiated by Jones Oliveira de Albuquerque on Tue Jun 1 18:39:53 EST 1999
- ...Albuquerque
- Aluno de Doutorado no DCC-UFMG
Jones Oliveira de Albuquerque
Tue Jun 1 18:39:53 EST 1999
 Departamento de Ciências Exatas
Departamento de Ciências Exatas 
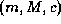 , onde m é o valor mínimo, M o máximo e c o grau de confidência do intervalo
, onde m é o valor mínimo, M o máximo e c o grau de confidência do intervalo 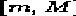 , por exemplo, (``muito alto'', ``alto'', ou ``baixo''). Estes graus de confidência mudam de acordo com o projeto e são baseados em dados históricos; se o time tem dados históricos precisos de suas tarefas realizadas e de grande relação com a estimativa então seu grau é ``muito alto'' e se ele não possui dados históricos ou se os dados não têm relação com a estimativa então seu grau é ``baixo''. Estes dados históricos podem ser coletados por monitoração de tempo, esforço e estimativas de projetos passados. Desta forma, tem-se um completo perfil do time de desenvolvimento. [
, por exemplo, (``muito alto'', ``alto'', ou ``baixo''). Estes graus de confidência mudam de acordo com o projeto e são baseados em dados históricos; se o time tem dados históricos precisos de suas tarefas realizadas e de grande relação com a estimativa então seu grau é ``muito alto'' e se ele não possui dados históricos ou se os dados não têm relação com a estimativa então seu grau é ``baixo''. Estes dados históricos podem ser coletados por monitoração de tempo, esforço e estimativas de projetos passados. Desta forma, tem-se um completo perfil do time de desenvolvimento. [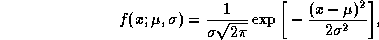
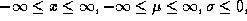
 é a média e
é a média e  o desvio padrão definido pelos graus de confidência.
o desvio padrão definido pelos graus de confidência.

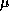 ) e diferentes graus de confidência (
) e diferentes graus de confidência (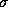 ).
).
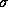 .
.
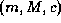 de forma que
de forma que 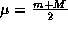 and
and 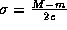 . A Tabela 1 apresenta os graus de confidência para valores inteiros de c, i.e., c=3 (``Muito Alto''), c=2 (``Alto'') e c=1 (``Baixo''). Os graus de confidência representam a possibilidade de uma estimativa estar no intervalo [m,M]. Na Figura 2, se tomarmos m=-2 e M=2, podemos comparar os diferentes graus de confidência associados com estes valores: Muito Alto para a curva mais interna (
. A Tabela 1 apresenta os graus de confidência para valores inteiros de c, i.e., c=3 (``Muito Alto''), c=2 (``Alto'') e c=1 (``Baixo''). Os graus de confidência representam a possibilidade de uma estimativa estar no intervalo [m,M]. Na Figura 2, se tomarmos m=-2 e M=2, podemos comparar os diferentes graus de confidência associados com estes valores: Muito Alto para a curva mais interna (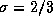 ), Alto para a curva do meio (
), Alto para a curva do meio (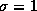 ) e Baixo para a curva mais externa (
) e Baixo para a curva mais externa (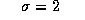 ).
).
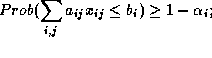
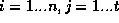 ,
, 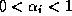 ,
, 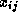 é uma variável binária e assume valor um (1) se a tarefa i é implementada pelo time j, n é o número de tarefas e t a quantidade de times dispoíveis,
é uma variável binária e assume valor um (1) se a tarefa i é implementada pelo time j, n é o número de tarefas e t a quantidade de times dispoíveis, 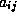 e
e 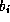 representam os parâmetros de restrição, e
representam os parâmetros de restrição, e 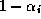 a probabilidade de certeza da restrição.
a probabilidade de certeza da restrição.
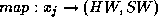 que satisfaça todas as restrições e minimize a função objetivo.
que satisfaça todas as restrições e minimize a função objetivo.
 como em [
como em [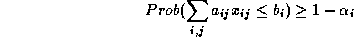
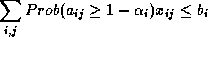
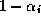 ) é transferida para os coeficientes
) é transferida para os coeficientes