|

|
Resolução de equação
Resolver as equações seguintes:
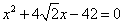
Aplicação das formulas classícas de determinação de raízes de equação do segundo grau ax²+bx+c:
b²-4ac=200, x1= 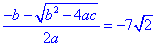 e x2= 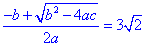 .
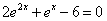
Podemos trocar exponential de x por uma outra variável X e resolver 2X²+X-6=0. As raízes são X1=-2 e X2=3/2.
As soluções da equação inicial são quando 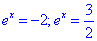 .
So tem uma solução quando 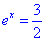 , x1=log(3/2).
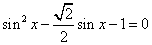
Podemos trocar seno de x por uma outra variável X e resolver 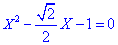 .
Raízes: 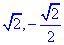 e temos 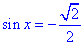 a resolver.
x1={-pi/4+2kpi,-3pi/4+2kpi}
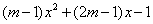
Bisseção
Determinar uma solução da equação:
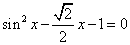
A partir de uma resolução gráfica e com o método da bisseção:
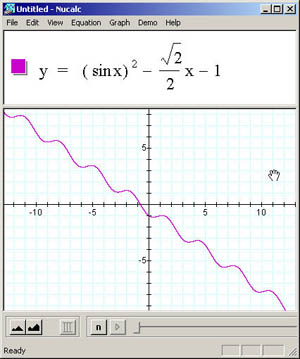
Representação gráfica:
A representação gráfica mostra que a função tem
uma raiz única e que ela é entre -1 e 0. |
Resultado da método da bisseção uma tolerância de 0,00390625 (1/256) |
 |
Intervalo [-1.000000, 0.000000], media: -0.500000
Intervalo [-1.000000, -0.500000], media: -0.750000
Intervalo [-1.000000, -0.750000], media: -0.875000
Intervalo [-0.875000, -0.750000], media: -0.812500
Intervalo [-0.812500, -0.750000], media: -0.781250
Intervalo [-0.781250, -0.750000], media: -0.765625
Intervalo [-0.765625, -0.750000], media: -0.757813
Intervalo [-0.757813, -0.750000], media: -0.753906
Resultado:
Intervalo [-0.753906, -0.750000], resultado: -0.751953
|
Zero de função
Método grafico
Localização gráfica das raízes das equações seguintes:
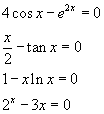
As equações podem ser transformadas em egualidades entre funções conhecidas:
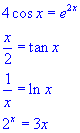
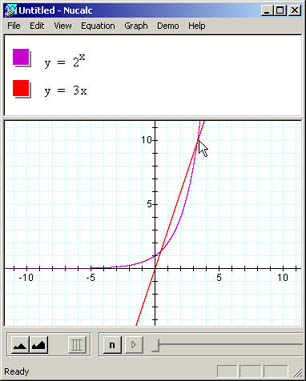
As raízes são dadas pelas intersecções entre os gráficos das funções:
Equação: 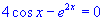 , raízes proximas de: 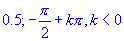
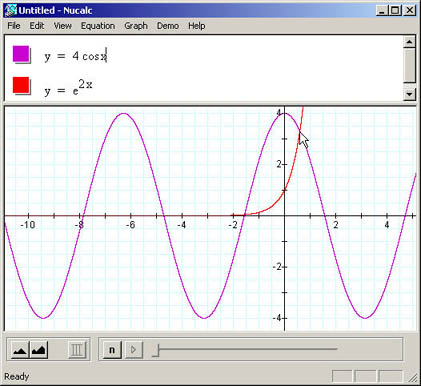
Equação: 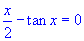 , raízes 0 e para k crescente se aproximando de: 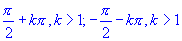
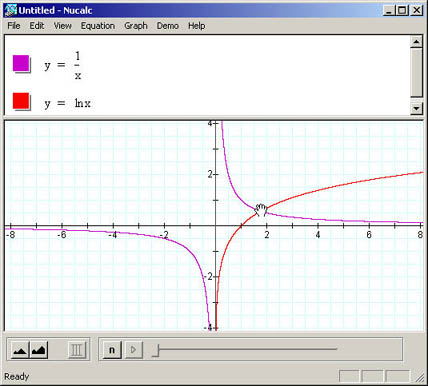
Equação: 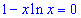 , raízes proximas de: 1.8
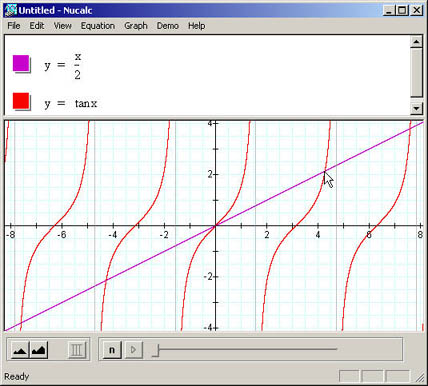
Equação: 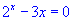 , raízes proximas de: 0.5 e 3.5
Algoritmos
Escrever procedimentos que determinam uma raíze de uma função f. Os valores
iniciais do procedimento são, além da função, um intervalo no caso da bisseção,
da secante e da falsa posição e um valor no caso do Newton-Raphson, uma tolerância
no caso da bisseção e um número de iterações no outros casos.
Solução em C:
|




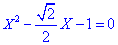 .
.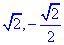 e temos
e temos 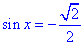 a resolver.
x1={-pi/4+2kpi,-3pi/4+2kpi}
a resolver.
x1={-pi/4+2kpi,-3pi/4+2kpi}

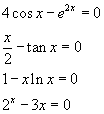
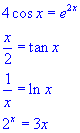
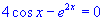 , raízes proximas de:
, raízes proximas de: 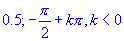

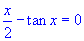 , raízes 0 e para k crescente se aproximando de:
, raízes 0 e para k crescente se aproximando de: 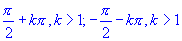

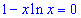 , raízes proximas de: 1.8
, raízes proximas de: 1.8
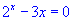 , raízes proximas de: 0.5 e 3.5
, raízes proximas de: 0.5 e 3.5